The funny thing about science is that it often behaves in ways that seem entirely irrational.
Take the strange phenomenon of simultaneous discovery: two or more thinkers come up with a new idea independently of one another at almost exactly the same time. The invention of calculus by Newton and Leibniz; Darwin and Wallace’s theory of evolution; Möbius and Listing’s discovery of the Möbius strip. What’s so odd about simultaneous discoveries — also known as “multiples” — is that they aren’t isolated events. They happen all the time.
Stranger still are those scientists who appear to have known things long before they could possibly know them. Stories of such people are incredibly rare and must be treated with caution. Like that popular misconception, the Eureka Myth, narratives of visionary foreknowledge tend to be apocryphal, presenting discovery as a result of individual insight rather than a process of investigation, calibration, and collaboration. But among the noise, do real visionaries — those who appear to ‘see’ the scientific future — really exist?
Simultaneous discovery and visionary foreknowledge hold a special place in the imagination because they appear to defy logic and reason. But humans, not machines, conduct science. And as such, discovery can be organic and surprising, unpredictable and messy. Discoveries are made, not found. If these stories really are true, how and why they happen — and whether they constitute an intrinsic part of scientific research or are a condition of temporally specific contexts — are important questions.
But they also make for fascinating stories.
For a while, no one noticed anything different. Palace Terrace Gardens was just an ordinary square in the heart of leafy west London. But when a new tenant moved into Number 8, things started getting strange.
This man was odd. He would pace the street into the early hours of the morning, muttering under his breath accompanied only by his dog. Some said the dog was more akin to a lab rat, that it was the subject of bizarre electrical experiments — its fur frayed from static charge. And then there was the coffin. Eight feet long and painted black, propped up by the attic window. For hours, the man would gaze into it, stopping only to make frantic notes. Occasionally his wife would join him; other times they would invite their friends to have a look too. What was in there? Was the man conducting some kind of freakish experiment, trying to reanimate dead matter?

The coffin in fact turned out to be a light box: a homemade device capable of producing an array of spectral colors. And the man was James Clerk Maxwell, the pioneer of electromagnetism. The above quirks are all true, but it goes to show how easy it is to paint a caricature of the lone, eccentric scientist using a few scraps of biographical information.
And yet. It seems as if Maxwell really was a brilliant visionary ‘ahead of his time.’ He discovered chaos theory. And he did so 100 years before it was even recognized as a science.
Maxwell’s path to chaos began when he turned his mind to one of the most mysterious objects in the cosmos — Saturn’s rings. For over two centuries astronomers had been baffled by their very existence. Were the discs solid or liquid? What were they made of? Why didn’t they break apart?
Applying existing mathematics in entirely new arrangements, Maxwell made some startling observations. He realized that a solid ring couldn’t be stable. Even the slightest perturbation would create an amplifying vibration that would destroy the entire structure. According to Maxwell, the rings, in spite of their continuous appearance, were in fact comprised of millions of smaller bodies orbiting the planet. For his efforts, Maxwell was awarded the prestigious Adams’ Prize for mathematics. But his work on Saturn’s rings had also got him thinking about statistically modeling dynamic systems.

In 1858, Maxwell read a paper by Rudolph Clausius that argued that gases are comprised of countless molecules moving around at immense speeds. The kinetic theory of gases could account for a vast range of observed phenomena. But for the theory to explain pressure, Clausius had to assume that the molecules in a gas of a given temperature all moved at the same speed. Maxwell thought that this could not be the case. He was convinced that the speed of individual molecules was random and defied the scientist’s powers of observation. The following year, Maxwell presented his work on the topic. His intervention was to devise a statistical function to calculate the overall distribution of molecular velocities and present them as an average. Viewed statistically, a gas’s behavior could thus be modeled as a probabilistic function.
This was a profound conceptual shift. It allowed scientists to describe a system of which their knowledge was incomplete. It also heralded the beginning of a new branch of physics, statistical mechanics.
Maxwell’s work also contained a radical implication about the relationship between mathematical laws and physical reality. It suggested that the second law of thermodynamics — the law that tells us that over time, the amount of useful energy in a closed system decreases — is not absolute. It is only highly likely. In theory, this means there is nothing to stop a gas’s molecules from becoming more ordered, say by returning to a perfume bottle after diffusing throughout a room. Taken even further, it suggests that heat can flow from a cold to hot body. Both cases represent a net decrease in entropy: a fundamental violation of thermodynamics. Maxwell would later expand on this idea in his infamous thought experiment known as ‘Maxwell’s Demon’. But at first, he didn’t see this implication. It seemed to emerge autonomously from the fabric of his mathematics.

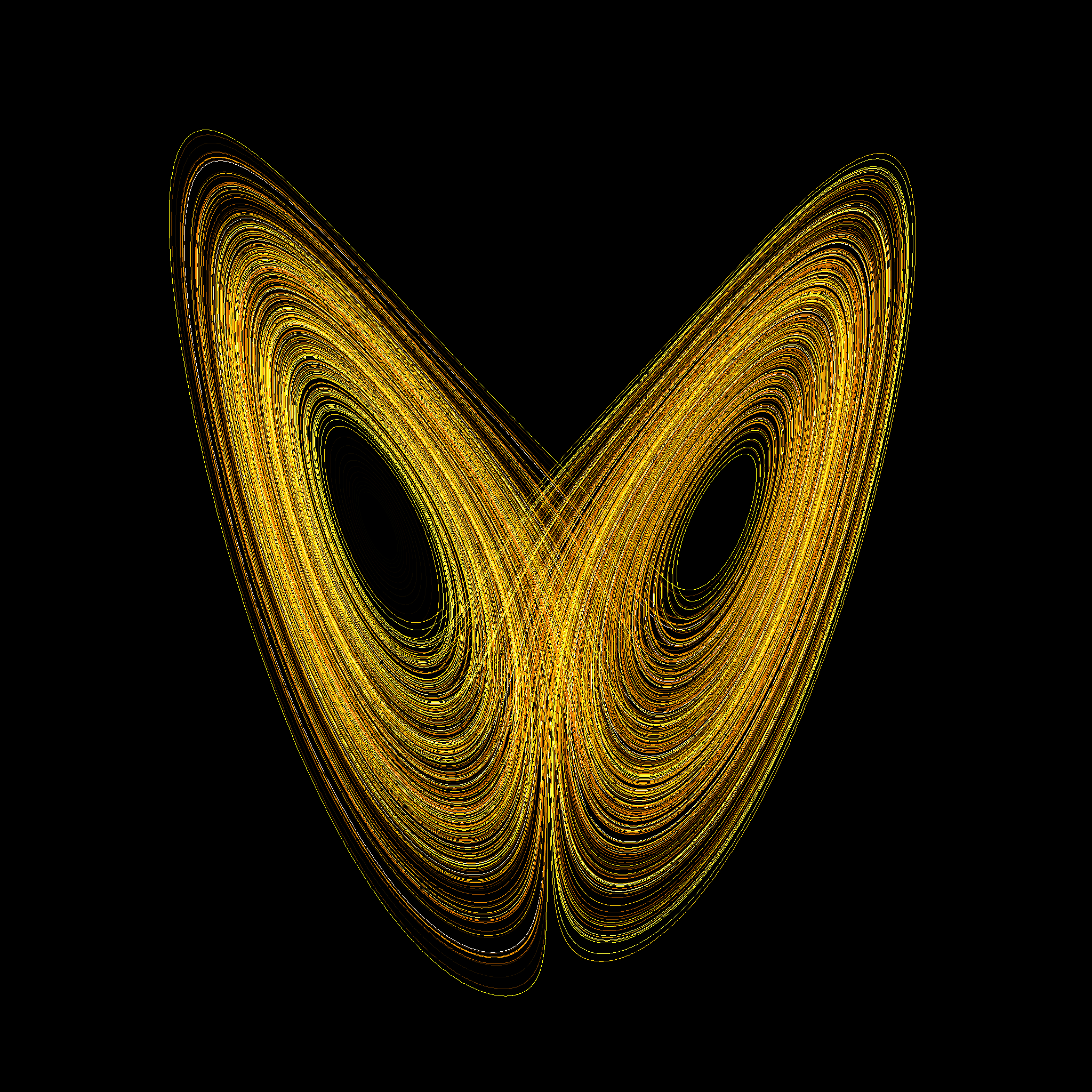
These ideas led Maxwell to the fundamental tenets of modern chaos theory. He saw that hidden order underlies chaotic systems and that self-organization, or local decreases in entropy, emerges spontaneously from chaos. Moreover, his work on Saturn’s rings prompted him to think about sensitive dependence upon initial conditions, popularly known as the ‘butterfly effect.’ By 1873, Maxwell had a profound understanding of chaotic systems:
“When the state of things is such that an infinitely small variation of the present state will alter only by an infinitely small quantity the state at some future time, the condition of the system, whether at rest or in motion, is said to be stable; but when an infinitely small variation in the present state may bring about a finite difference in the state of the system in a finite time, the condition of the system is said to be unstable.”
Decades before anyone else it seems, Maxwell understood chaos. Yet were his ideas truly ‘visionary,’ or part of a more complex framework of discovery? And what does it mean when visions strike more than one ‘lone genius’ simultaneously?
In the early 1820s, a Hungarian mathematician called Janos Bolyai came up with an idea that would revolutionize geometry. At the same time, 1500 miles away in the Russian city of Kazan, Nikolai Lobachevsky would make the same discovery. And then a third man, Karl Friedrich Gauss — dubbed the ‘Prince of Mathematics’ — would claim that he too had also come to the same conclusion. And not only that: he had been thinking about this idea for years prior to both Bolyai and Lobachevsky.
The idea stemmed from a challenge to the laws of Euclidean geometry, the basic laws of shape we all learn in school. The internal angles of a triangle add up to 180 degrees; space is isomorphic and flat. It’s the mathematics that relates to our subjective experience of space and which allow it to be mapped in three equal dimensions — x, y and z.
Bolyai and Lobachevsky began to challenge the supposed inviolability of these assumptions: in particular, Euclid’s parallel postulate. This says that two straight lines, parallel to each other and extending indefinitely, will never meet. Bolyai and Lobachevsky disagreed. They began to re-evaluate the notion of ‘straightness’ and realized that it only made sense in flat, even space.
They imagined straight lines not as ruler-edges on flat surfaces but rather as lines on a curved surface, such as a saddle shape. This geometry, termed “hyperbolic,” deals with spaces of constant negative curvature — where every plane through a point is drawn inwards. Lines traced on such spaces violate Euclid’s ancient maxim. A hyperbolic triangle’s internal angles total less than 180 degrees, while parallel lines diverge away from each other.
The corollary of this is also true: if two vertical lines are traced on the Earth’s surface, both beginning at right angles to the equator, they will eventually meet at the same point, the North Pole. These lines, fixed to a spherical, two-dimensional space, are ‘straight.’ Yet the shape they trace — a geodesic triangle — contains three interior right angles adding up to 270 degrees.
The invention and discovery of so-called ‘non-Euclidean’ geometry was a profound conceptual shift. Without it, Einstein’s relativity wouldn’t exist. Bolyai was certain of the uniqueness of his discovery: “I have created a new universe from nothing,” he wrote to his father in 1823. Similarly, in an 1824 letter to Franz Taurinus, Gauss claimed that he had found “a curious geometry, quite different from ours, but thoroughly consistent.” Lobachevsky, meanwhile, first reported his findings to the University in Kazan in February 1826, but wasn’t published until a few years later.
All three men came up with the same idea, at the same time, totally independently. All thought they were alone. And this all happened well before the modern era of global connectivity and interdisciplinary research. Was the time just right? Was something ‘in the air’?
Well, in a way, yes. In 1960, a study by Robert Merton claimed, “the pattern of independent multiple discoveries in science is in principle the dominant pattern, rather than a subsidiary one.” Subsequent research has come to the same conclusion. In a survey of hundreds of new patent applications, Mark Lemley found that “almost all of them [were] invented simultaneously or nearly simultaneously…independently of each other.”
Comparable studies invariably affirm the same thing: simultaneous discovery isn’t the exception; it’s the norm. In popular accounts of scientific history, scientists are still generally painted as the romantic outsider whose visionary brilliance sparks new ideas ex nihilo. But in reality it doesn’t work this way. Scientists, as Lemley writes, “build on the work of those who came before, and new ideas are often ‘in the air,’ or result from changes in market demand or the availability of new or cheaper starting materials.”
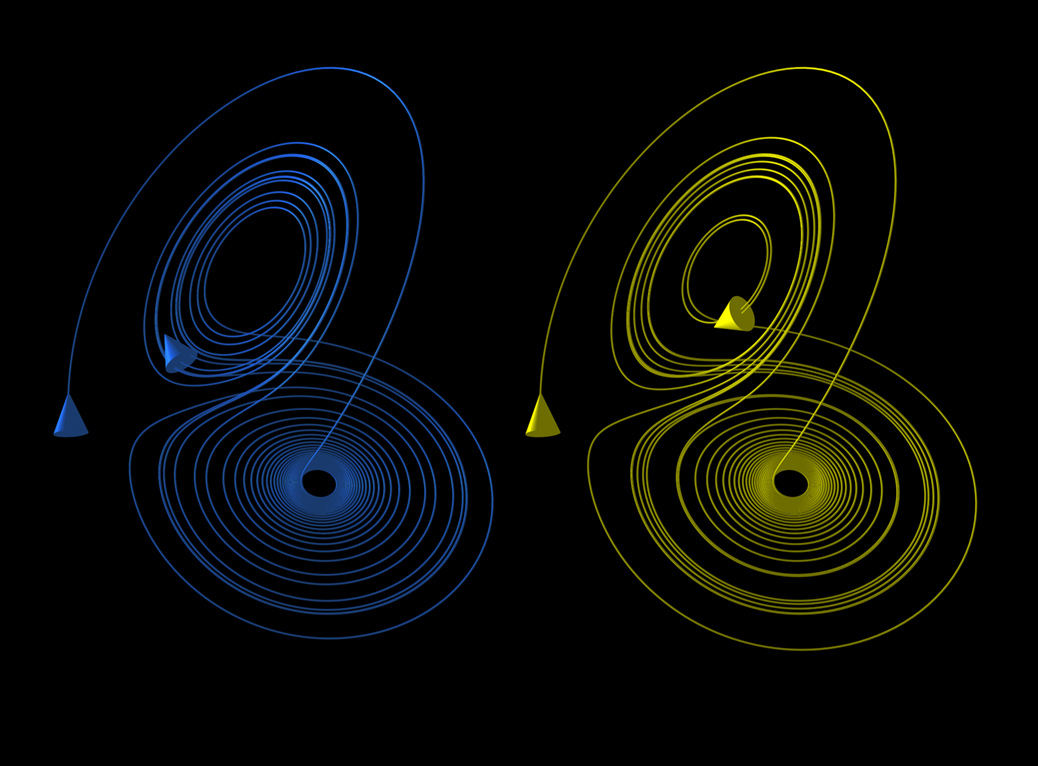
Synchronicity in science suddenly seems less surprising. Given that new ideas are so reliant on technology and the ability to connect emergent and disparate areas of knowledge, it’s almost inevitable that discoveries will occur multiply. What’s more, it’s a trend that has been increasing over time.
But what about cases such as Maxwell’s, where new ideas are so distinct from their surrounding intellectual context as to appear nonsensical? In these cases, future science seems quite literally made, not found.
Some argue that, unlike the prevalence of simultaneous discovery, individual insight is a phenomenon consigned to science’s past. A 2007 study found that a defining trend of contemporary research has been the overall shift from knowledge produced by individuals to teams. Analyzing nearly 20 million papers from the last five decades, the researchers found that teams produced both the vast majority of “exceptionally high impact research” and work dominating citation distribution. This is perhaps due to greater recognition of the role lab assistants and technicians play in gathering data. But it’s also a phenomenon driven by the increased subdivision of disciplines.
Northwestern professor Ben Jones suggests as much in a paper looking at the changing conditions of innovation. Jones claims that over time, flashes of scientific insight have declined — a result of the multidisciplinary nature of experimental work and the increasing specialization of knowledge. “If one is to stand on the shoulders of giants,” he writes, “one must first climb up their backs, and the greater the body of knowledge, the harder this climb becomes.”
Our skepticism towards narratives of visionary genius also stems from a greater awareness of how science is reported. Histories are constructed accounts that tend to mythologize the individual in place of the messy and evolving reality of scientific plurality. This is not to take away from Maxwell’s extraordinary intuition, nor is it to suggest science is practiced the same way throughout history. 19th century Britain certainly had fewer professional scientists than today, working in broader knowledge bases with a lower overall body of specialized information. If an individual was going to make a revolutionary discovery, then was as good a time as any.
But Maxwell also didn’t work in a vacuum. He processed information analogically, taking ideas from disparate branches of mathematics and applying them in new ways. He conducted experiments with other scientists, went to conferences, conferred about speculative ideas. And his own models contained implications of which he wasn’t always aware. Implications that bubbled under the surface but weren’t fully recognized until the fog of intellectual confusion had time to dissipate.
The most surprising thing then about Maxwell’s understanding of chaos is that it doesn’t fit the standard model of simultaneous discovery. He just happened to connect the dots in the right way. He was able to do so because he was a brilliant scientist, but there were numerous advantageous variables at play as well.
As such, stories of visionary science are problematic because they take a singular view of multiplicity. Maxwell’s case was a statistical anomaly, and one that itself can be considered multiple given his reliance on other’s work. But statistics can help us to better understand ‘insight’ and simultaneity and refine the way we construct historical narratives. Because, to use a Maxwellian analogy, scientific practices are themselves dynamical systems: constantly in flux and comprised of countless variables. We can’t trace these variables individually. But we can map them statistically by writing stories that more accurately approximate the unstable, fraught conditions of discovery.